Possible chess knights movements using minimax algorithm

While at high school, I had been assigned to make a two-person game in Artificial Intelligence studies based on chess figure – knight, where one player is human and other is a computer on 4×4 field. Also, you can’t step on the same field where you or computer has already been. At first, I had to do that by hand – get all possible moves. After that, I needed to make a working example and I did it in Ruby.

In this article, I’ll be explaining basic things, such as:

• how knight can move
• basic information about A.I.
• the beast called recursion
• what is the minimax algorithm
• loading start game grid
• generating movement tree
• printing for visibility
• making basic moves

The theory part

I will start off by explaining some essential theory which you might already know, if so – skip to the next chapter.

How does a chess knight move?

If you ever have played chess, then you know that knight can be a very powerful and dangerous piece on your chess table. From all chess pieces, the knight moves the most unusual way. It can move to a square that is two squares horizontally and one square vertically, or two squares vertically and one square horizontally. So, if the knight has space, it can move 8 different squares from its current position.

Basic information about Artificial Intelligence

Let’s start by explaining each word as it is. Artificial means not real, fake, made or produced, that is mostly self-explanatory. Intelligence, on the other hand, has a quite harder explanation. It could mean huge knowledge, the capability to learn something, it is associated with secret agencies and government itself and so on. But how these words are combined in IT science? In my opinion, Artificial Intelligence is the capability of non-living things to think, learn, analyze and then act based on the information and/or situation.

Nowadays, you can see movies full of AI Integration Examples, AI robots and services, planes and other things which can do amazing things, but the situation in real life is quite the opposite, at least in full-scale robotics. There are self-automated cars and planes, but making human-like robot is only in future. That is because, first of all, robots should be able to learn – and how do you learn? By experimenting, doing things and so on. But what makes you understand that you have learned/succeeded? It is the result itself. For example, you see fire, you touch it and it is hot, it burns you and you decide not to touch it again. But how would a robot know that? It doesn’t feel the pain, doesn’t have conscious to tell good and bad aside. That is why A.I. needs some kind of data to be based on.

Why am I telling all this? Quite simply, to play against the computer, it should know what to do, how to react on your moves and decide the best possible move. That is why we, the programmers of a new world, need to write some gibberish code to guide our fellow computer friend in the world of unknown. But then raises a question – hey, you programmed it, that doesn’t make it A.I. – self-thinking. That is true, but think of your favourite FPS game where the computer could play against you, it is the same, but they act like humans, don’t they? It is how you programmed it – make it very complex, evolve the code and maybe, someday it will start writing code for himself(itself). So, to play against my knight-computer we need to tell it how to play. In my assignment, I needed to use the minimax algorithm for computer decision making the process.

Few words about recursion

Recursion is a programming concept, which, by its idea, lets function call itself. It is pretty easy to understand, however, implementing such a concept can get you some headache, because it has a high chance you will go in an infinite loop and get stack level too deep error. To avoid this, you clearly need to know what you want to do, what is the next step for function and, more importantly, what is the stopping condition/point. For me, the ending point was the hardest part while I was learning the LISP programming language.

Example factorial function:

def fact(n)  
  if n > 1
    n * fact(n - 1)
    # puts n

    # In theory, that puts is only executed when deepest level -1 of recursion is reached,
    # that is, when fact returns 1 and steps back.
    # In this example it would break recursion because fact works on returned values, puts returns nil
  else
    1
  end
end

As you can see, I have condition check for n which would decide if it is stopping point or next function call (n – 1). What recursion also means is that it goes to deepest possible level (endpoint you decide) and goes back level by level returning value from a deeper level so you can intercept value. As useful as recursion is, it shouldn’t be used when a simple loop can do the thing simpler.

What is the minimax algorithm?

Minimax algorithm tries to minimize the risk of losing. In short, the computer will play at it’s best to not let you win. For minimax algorithm to work, the game needs a tree of all* possible moves for the computer to decide which route through a tree to take.

*All possible moves in this game because it is short, but in such games like standard chess it is not possible because of the huge scaling – 10^120 possible variations, so most of the times tree is being generated dynamically.

Tree generating happens by code (game conditions) itself and it doesn’t involve algorithm directly but while the tree is being generated, the algorithm starts its work by setting first nodes state(min/max). In the next levels of the tree (deeper ones) state is based on previous levels state (opposite of it).

Example:

If we set the first nodes state as min, next level nodes must be the max, after that level, min and so on.

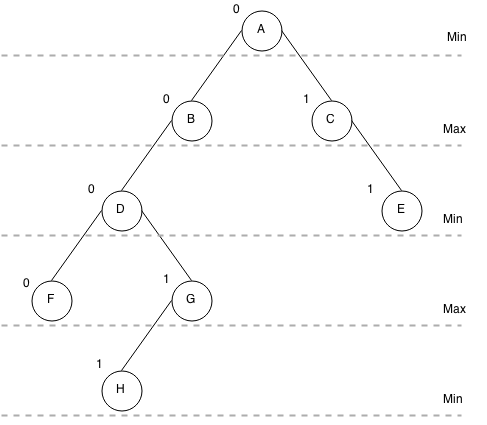
While the tree is being generated, the algorithm is searching for deepest level, when found, it sets that nodes rank (0/1) based on nodes state. If the state is min, the rank will be 1, if max then 0. After that, tree generation continues by backing up one level (because of recursion), algorithm checks if there are all child nodes with the rank set (which means it is looked), if so, the algorithm sets rank based on state (min/max). If there are any child nodes without rank set, the algorithm follows tree generation process (it will go deeper due recursion), and repeats itself. When all those children have rank set and algorithm is a point where a parent has 2 or more children, it chooses rank between children to rank values based on current levels state.

Example:

Let’s do this step by step:

• Algorithm finds all end nodes (H, F, E) and sets their value based on state: min=1, max=0
• Next step on E branch, the algorithm moves back to C, checks for all children ranks and picks a maximum of them, so [1].max is 1.
• Moving to A, the algorithm finds that B node is missing rank, let’s find it.
• H is 1, so G must be 1 too, because it has only one child ([1].max)
• F is 0, but what about D? It has min state, so: [0, 1].min means that D is 0.
• Now, we can get B, which is 0 because D is 0 too. ([0].max)
• Finally, we can get A which has a child’s B and C, so [0, 1].min is 0.

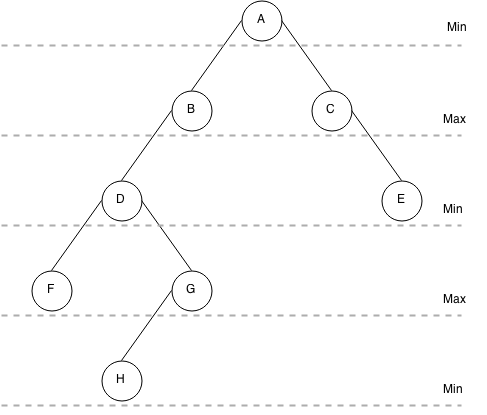
When all that is done, the first node should have 0 or 1 as rank. Based on that rank, the computer will determine the best move in each position.

The programming part

For this blog post, I’ll be using reduced and cleaner code as it was for the actual game. The program will consist of 3 files:

• main.rb which will launch this simple application.
• grid.rb for Grid class and manipulations with grid.
• tree.rb for Tree class that will generate a tree and implement minimax algorithm.

Main

Comments in code are self-explanatory

class Main  
  # Some constants for easier use
  PLAYER_1 = 0
  PLAYER_2 = 1

  CURRENT_POSITION = 0
  CURRENT_X = 1
  CURRENT_Y = 2

  # Creates some default 4x4 game grid with 2D arrays
  def make_grid
    grid = [
      [0, 1, 0, 0],
      [0, 4, 0, 0],
      [0, 0, 3, 0],
      [0, 0, 2, 0]
    ]

    # Players location [player_info1, player_info2] where player_info[index, x, y], last even and odd values from grid
    players = [[3, 2, 2], [4, 1, 1]]

    # Creates first game grid
    grid_object = Grid.new(grid, players[PLAYER_1], players[PLAYER_2])
    # Prints out starting grid
    print_grid(grid_object.grid)
    # Generates tree
    tree_object = Tree.new.generate(grid_object.grid, players[PLAYER_1], players[PLAYER_2])
    # Prints full tree
    print_tree(tree_object)
  end

  private
  # Helper printing methods, fugly.
  def print_grid(grid, right = '  ')
    grid.each do |i|
      val = ''
      i.each do |j|
        val = val + "[#{j > 0 ? j.to_s.rjust(2, ' ') : '  '}] "
      end
      puts "#{right}#{val}"
    end
    puts "#{right}-------------------"
    ''
  end

  def print_tree(tree_object, right = '  ')
    if(tree_object)
      print_grid(tree_object.grid, right)
      right = right + '  '
      tree_object.moves.each do |node|
        print_tree(node, right)
      end
    end
  end
end

# Game initializer
require_relative 'tree'  
require_relative 'grid'

Main.new.make_grid

Grid

Comments in code are self-explanatory

class Grid < Main  
  # So we access from outside
  attr_accessor :grid, :moves, :state, :rank

  # Sets default values for object
  def initialize(grid_array, player1_info, player2_info)
    # Needs to_s and eval because for some reason Ruby keeps it by reference even if I dup or clone
    @grid = eval(grid_array.to_s)
    # Will hold all possible moves based on current grid
    @moves = []
    # State - min/max
    @state = ''
    # Rank - 0/1
    @rank = -1

    # Sets both player locations on grid, player_info = [index, x, y]
    @players = [player1_info, player2_info]
    set_player_coords(player1_info)
    set_player_coords(player2_info)
  end

  # Helper methods
  # Get player info - [index, x, y]
  def player_info(player)
    @players[player]
  end

  # Finds who's move it is
  def current_player
    @players[PLAYER_1][CURRENT_POSITION] < @players[PLAYER_2][CURRENT_POSITION] ? PLAYER_1 : PLAYER_2
  end

  # Changes current players info
  def current_player_set(array)
    @players[current_player] = array
  end

  # Finds current players index
  def current_index
    @players[current_player][CURRENT_POSITION]
  end

  # Finds current players x
  def current_x
    @players[current_player][CURRENT_X]
  end

  # Finds current players y
  def current_y
    @players[current_player][CURRENT_Y]
  end

  # Determines best next move for computer
  def find_best_way
    if @state == 'max'
      way = moves.max{ |a, b| a.rank <=> b.rank }
    elsif @state == 'min'
      way = moves.min{ |a, b| a.rank <=> b.rank }
    end
  end

  # Sets state based on previous state
  def set_state(prev_state)
    if prev_state == 'max'
      @state = 'min'
    elsif prev_state == 'min'
      @state = 'max'
    end
  end

  # Sets rank based on current state
  def set_rank
    ranks = @moves.collect{ |x| x.rank }
    if @state == 'max'
      @rank = ranks.max
    elsif @state == 'min'
      @rank = ranks.min
    end
  end

  # Finds all possible moves from current move in specific grid
  def self.find_valid_movement(grid, x, y)
    valid_coordinates = [
      [-2,-1],[-1,-2],[ 1,-2],[ 2,-1],
      [-2, 1],[-1, 2],[ 1, 2],[ 2, 1]
    ]
    move_to = []

    valid_coordinates.each do |array|
      x_coordinate = array[0] + x
      y_coordinate = array[1] + y
      next if outside_area?(x_coordinate, y_coordinate)
      move_to << [x_coordinate, y_coordinate] if grid[x_coordinate][y_coordinate] == 0
    end

    move_to
  end

  # Helper method to check coords
  def self.outside_area?(x, y)
    x < 0 || y < 0 || x > 3 || y > 3
  end

  private

  def set_player_coords(player_array)
    position = player_array[CURRENT_POSITION]
    x = player_array[CURRENT_X]
    y = player_array[CURRENT_Y]

    @grid[x][y] = position
  end
end

Tree

Comments in code are self-explanatory

class Tree < Main  
  # Generates tree from given grid and locations, first state is max, returns full tree
  def generate(grid, player_1, player_2)
    new_grid_object = Grid.new(grid, player_1, player_2)
    new_grid_object.set_state('max')
    generate_moves(new_grid_object)
    new_grid_object
  end

  # Recursive function
  def generate_moves(grid_object)
    # Finds all possible moves based on current grid
    move_to = Grid.find_valid_movement(grid_object.grid, grid_object.current_x, grid_object.current_y)

    # Iterates through all possible next moves
    move_to.each_index do |i|
      # Determines where to put next move based if next_position is odd or not
      next_position = grid_object.current_index+2
      new_player_info = [next_position, move_to[i][0], move_to[i][1]]
      player_1 = next_position.odd? ? new_player_info : grid_object.player_info(PLAYER_1)
      player_2 = next_position.odd? ? grid_object.player_info(PLAYER_2) : new_player_info

      # Creates new grid based on new moves
      new_grid_object = Grid.new(grid_object.grid, player_1, player_2)
      # Adds new grid to old grids moves array
      grid_object.moves << new_grid_object
      # Sets new grids state based on previous state
      new_grid_object.set_state(grid_object.state)
      # Goes deeper in recursion with newly created grid
      generate_moves(new_grid_object)
      # When recursion has come back (reached deepest level), old grid gets rank based on childs it has
      grid_object.set_rank
    end

    # When reached deepest level of tree, sets rank based on state
    set_last_rank(grid_object) if move_to.empty?
  end

  private

  def set_last_rank(grid_object)
    if grid_object.state == 'min'
      grid_object.rank = 1
    else grid_object.state == 'max'
      grid_object.rank = 0
    end
  end
end

Launching tree generator

Write ruby main.rb, where you have to save main.rb and output, should be the same as this: example output

How to play?

Well, this example isn’t completely playable because it doesn’t have the functionality. I won’t be talking about that in here, but if you wish, you can visit GitHub page and download little bit messier and undocumented full code.

Please check another examples of the AI Services and Integration we have.

Diatom Enterprises – is a Latvian Software Development Company. Please do not hesitate contact us if you need any needs connected with the AI Development Services and Integrations

AIAI Development ServicesAI Services and Integrationalgorithmsartificial intelligenceminimaxprogrammingrecursionRoRruby